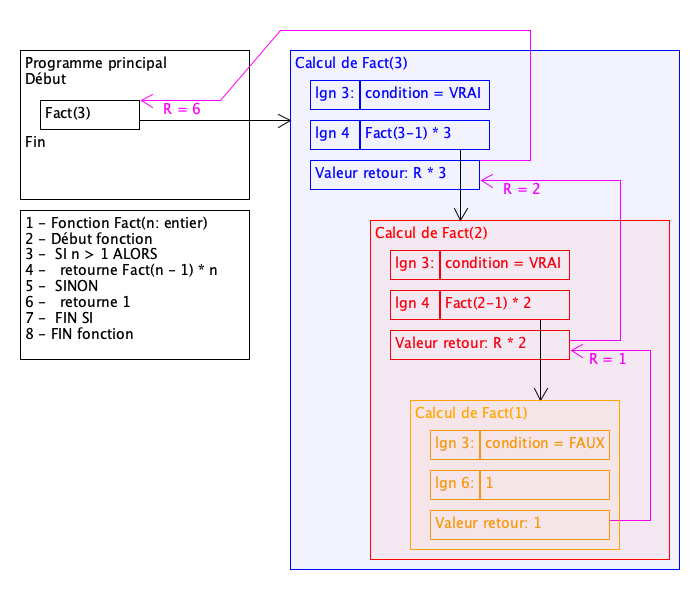
La récursivité consiste a écrire une fonction qui s’appelle elle-même afin de réaliser des calculs.
Le calcul de la fonction factorielle s’écrit ainsi:
\(n! = 1 \times 2 \times ... \times n\)
Par exemple:
\(3! = 1 \times 2 \times 3\)
Il est assez facile d’en déduire que:
\[4! = 1 \times 2 \times 3 \times 4\]
\[4! = 3! \times 4\]
On peut alors généraliser:
\[n! = (n - 1)! \times n \]
Sachant que \(1! = 1\)
La fonction factorielle peut s’écrire ainsi:
1 : Fonction Fact(n: entier)
2 : Début fonction
3 : SI n > 1
4 : retourne Fact(n - 1) * n
5 : SINON
6 : retourne 1
7 : FIN SI
8 : FIN fonctionL’exécution se fait en appelant la fonction Fact.

Créer un algorithme permettant d’afficher un compte à rebours de manière récursive
Modifier l’algorithme précédent pour créer un algorithme permettant d’afficher un comptage de 1 à N de manière récursive.
Réaliser la conversion de décimal vers binaire d’un nombre peut se faire de manière récursive.
Par exemple: \((25)_{10} = (?)_2\)
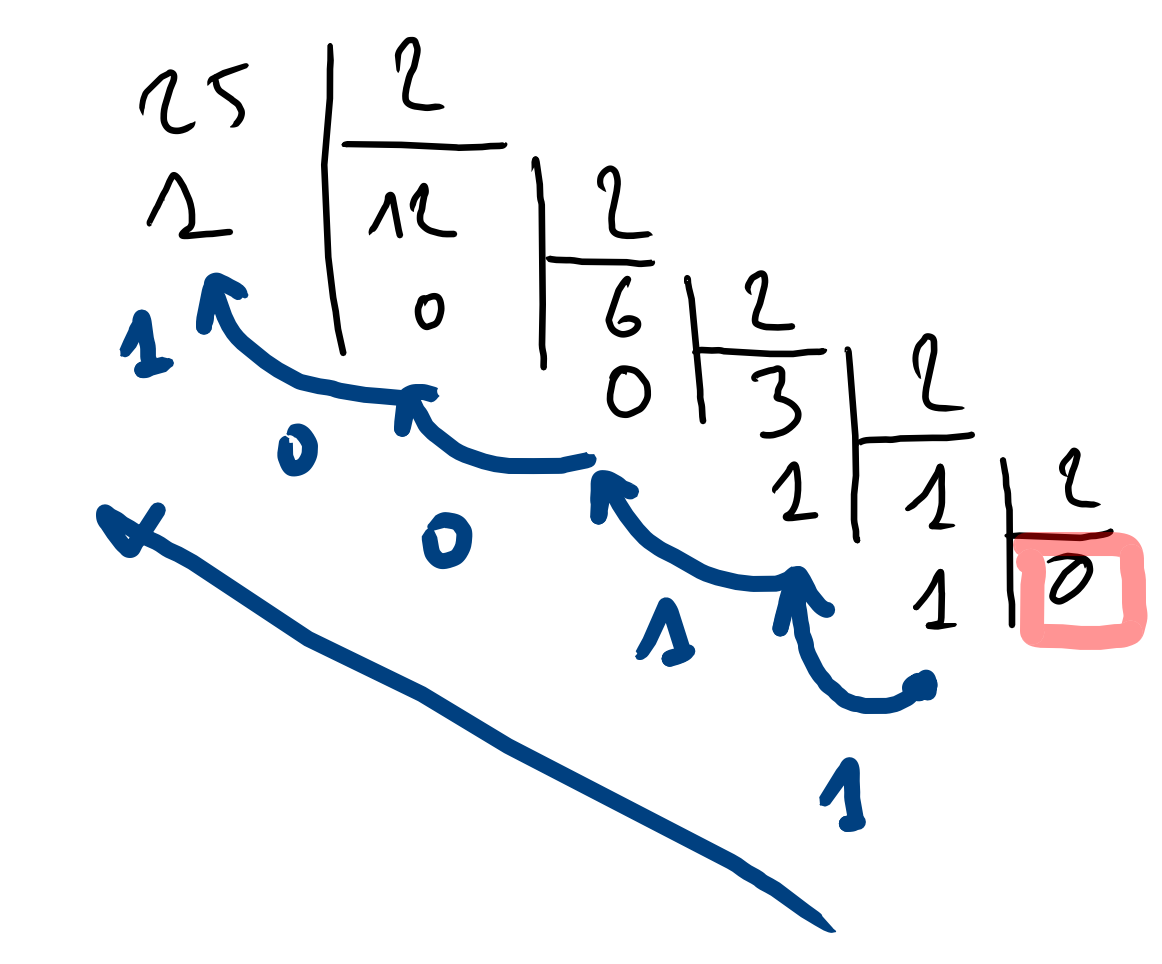
Ceci peut se représenter ainsi:

Écrire l’algorithme permettant de réaliser cette opération de conversion.
Utiliser l’outil de programmation en pseudo-JS
Placer les fichiers dans un dossier nommé
exercices-recursivite
Écrire l’algorithme permettant de calculer la somme des éléments d’un tableau de manière récursive.
La suite de Fibonacci est définie comme suit :
\[ F_n= \left\{ \begin{array}{ccr} 1 & si~n \lt 2 \\ F_{n-1}+F_{n-2} & si~n \ge 2 \\ \end{array} \right. \]
Ecrire un algorithme récursif calculant Fib(n)
Soit la suite définie par :
\[ U_n= \left\{ \begin{array}{ccr} 1 & n \lt 2 \\ 3U_{n-1}+U_{n-2} & sinon \\ \end{array} \right. \]
Ecrire un algorithme récursif permettant de calculer le nième terme de la suite.
Un nombre N est pair si (N-1) est impair,
et un nombre N est impair si (N-1) est pair. Ecrire deux
fonctions récursives mutuelles pair(N) et
impair(N) permettant de savoir si un nombre N est pair et
si un nombre N est impair.
Écrire l’algorithme permettant de trouver le plus grand nombre dans un tableau de manière récursive.
Un mot est un palindrome si on peut le lire dans les deux sans de gauche à droite et de droite à gauche. Exemple ROTOR est un palindrome. Ecrire un algorithme récursif permettant de vérifier si un mot est palindrome.
Étant donné deux séquences, trouvez la longueur de la sous-séquence la plus longue présente dans les deux. Une sous-séquence est une séquence qui apparaît dans le même ordre relatif, mais pas nécessairement contiguë.
Par exemple, “abc”, “acg”, “bde”, “adg”, “abefg”, etc sont des sous-séquences de “abcdefg”. Ecrire une fonction pour compter la plus longue sous-séquence.