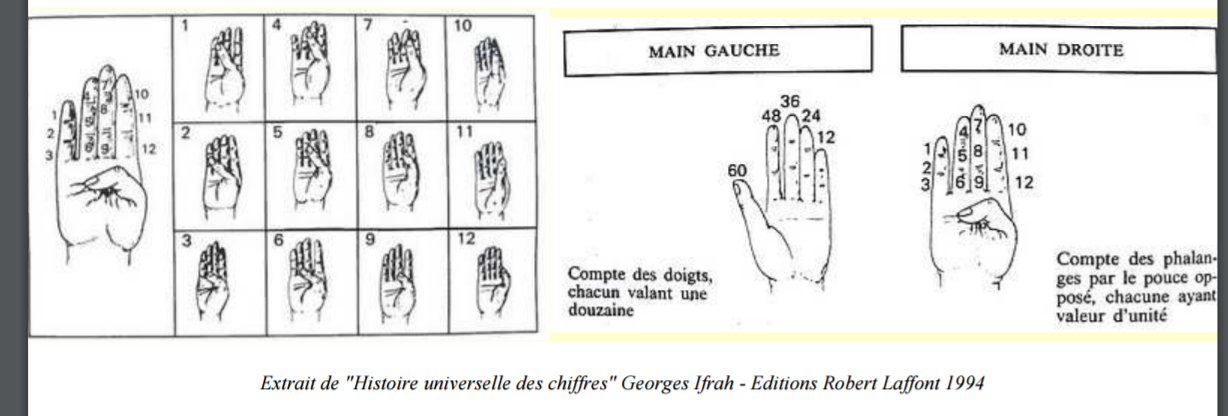
Ensemble d’éléments qui permettent d’écrire, de lire et de définir des nombres:
Des dizaines de systèmes ont été utilisés
Dans un système de numération positionnel: nombre de symboles (de chiffres) qui sont utilisables pour représenter les nombres.
10 chiffres, soit de 0 à 9
Numération binaire: 2 chiffres
Les nombres comme on les connait sont les chiffres indo-arabes, soit :
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
S’utilise généralement en base 10 des nombres.
Pour différencier: Or, pour faciliter la compréhension, ces mêmes
chiffres seront utilisés tout au long de la fiche. Pour faire une
différence au niveau de la base utilisée, on utilisera l’indice comme
référence:
57612 = 576 en base 12

On compte de 0 à 9
On compte de 0 à 1
| Puissance de 2 | Valeur décimale |
|---|---|
| 20 | 1 |
| 21 | 2 |
| 22 | 4 |
| 23 | 8 |
| 24 | 16 |
| 25 | 32 |
| 26 | 64 |
| 27 | 128 |
| 28 | 256 |
| 29 | 512 |
| 210 | 1024 |
| 211 | 2048 |
| 212 | 4096 |
| 213 | 8192 |
| 214 | 16384 |
| 215 | 32768 |
| 216 | 65536 |
| BIN | DEC | OCT | 2P |
|---|---|---|---|
| 000 | 0 | 0 | |
| 001 | 1 | 1 | 20 |
| 010 | 2 | 2 | 21 |
| 011 | 3 | 3 | |
| 100 | 4 | 4 | 22 |
| 101 | 5 | 5 | |
| 110 | 6 | 6 | |
| 111 | 7 | 7 |
On compte de 0 à F:
0 1 2 3 4 5 6 7 8 9 A B C D E F
| BIN | DEC | HEX | OCT | 2P |
|---|---|---|---|---|
| 0000 | 0 | 0 | 00 | |
| 0001 | 1 | 1 | 01 | 20 |
| 0010 | 2 | 2 | 02 | 21 |
| 0011 | 3 | 3 | 03 | |
| 0100 | 4 | 4 | 04 | 22 |
| 0101 | 5 | 5 | 05 | |
| 0110 | 6 | 6 | 06 | |
| 0111 | 7 | 7 | 07 | |
| 1000 | 8 | 8 | 10 | 23 |
| 1001 | 9 | 9 | 11 | |
| 1010 | 10 | a | 12 | |
| 1011 | 11 | b | 13 | |
| 1100 | 12 | c | 14 | |
| 1101 | 13 | d | 15 | |
| 1110 | 14 | e | 16 | |
| 1111 | 15 | f | 17 |
1 - Écrire en base 2 les nombres suivants :
56; 115; 152; 524; 615; 1020.
2 - Écrire en base 16 les nombres suivants :
56; 115; 152; puis, 524; 615; 1020.
3 - Écrire les nombres hexadécimaux en décimal, puis en binaire :
A6F; 128; 3AD; FFF; FAB; EC7; 100; DDD.
4 - Classer dans l’ordre croissant les nombres suivants :
11111001(2) ; 1101(10) ; 1101(16) ; 1000(16) ; 1000(2) ; 10000 (10)
5 - Multipliez 110 0011 par 2. Que remarque-t-on ? En déduire ce qu’il se passera lors d’une division par 2
Calculer la valeur décimale de:
Pour chacune de ces valeurs, calculer:
| Hexa | Binaire | Calcul / valeur base 10 |
|---|---|---|
| 1F | 0001 1111 | 2^5 - 1 : 32 - 1 = 31 |
| EF | 1110 1111 | 14x16^1 + 15x16^0 = 239 |
| C2 | 1100 0010 | 12x16^1 + 2 = 194 |
| CAFE | 1100 1010 1111 1110 | 12x16^3 + 10x16^2 + 15x16^1 + 14 |
| BABA | 1011 1010 1011 1010 | 11x16^3 + 10x16^2 + 11x16^1 + 10 |
| F0 | 1111 0000 | 240 |
| F1 | 1111 0001 | 241 |
| F8 | 1111 1000 | 248 |
Numération et codage/Conversion décimal à binaire — Wikiversité
Convertir en base 2
bits : 0 ou 1
octets = 8 bits
Byte = mot de X bits
Par convention, un byte est un mot de 8 bits
| Puissance de 2 | Symbole |
|---|---|
| 2^10 | K |
| 2^20 | M |
| 2^30 | G |
| 2^40 | T |